无人解开的数独
无人解开的数独,不仅包括非常困难的题目,也包括还没有人尝试挑战的数独。
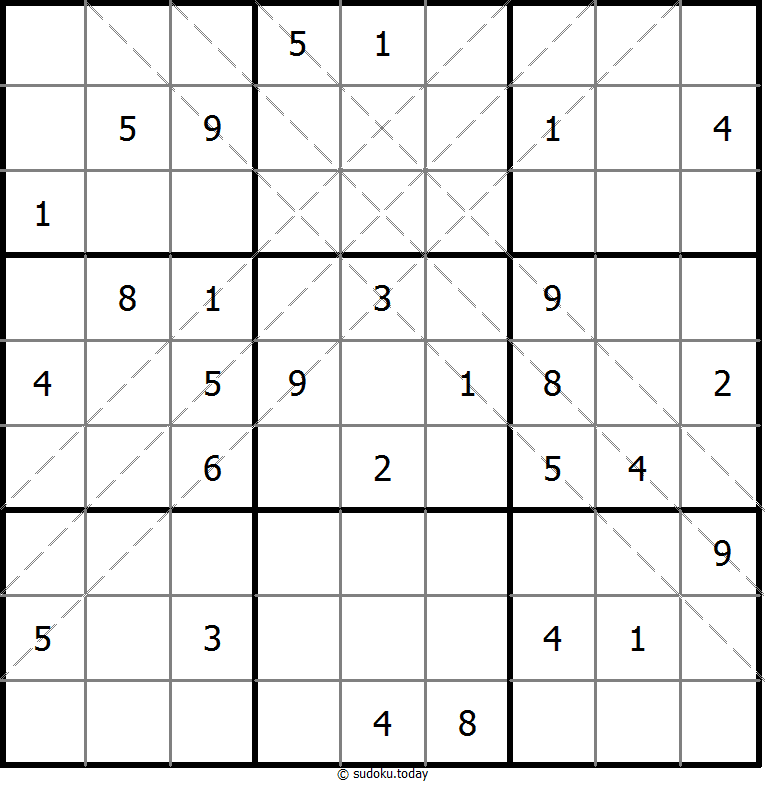
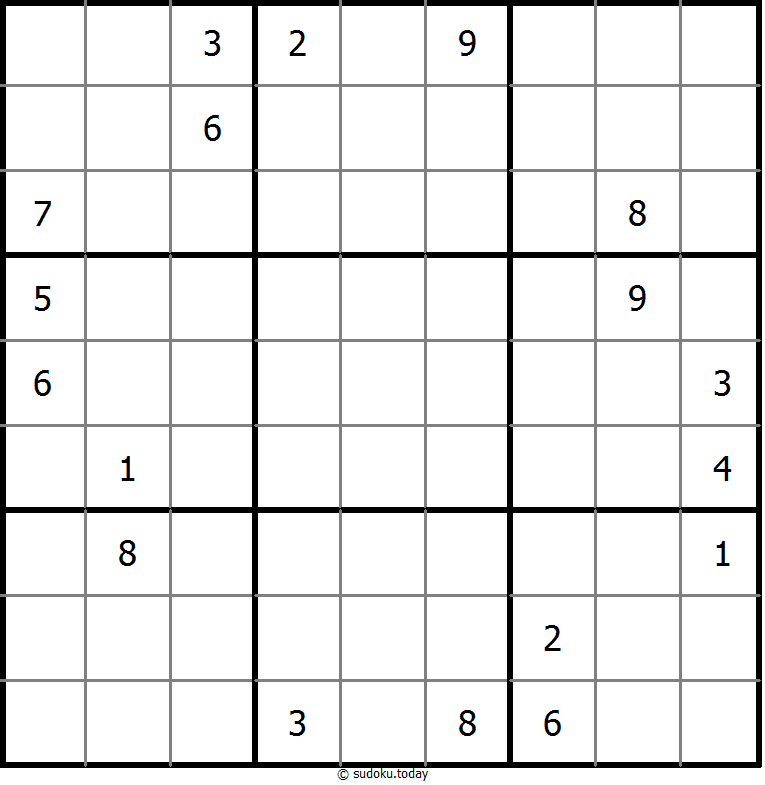
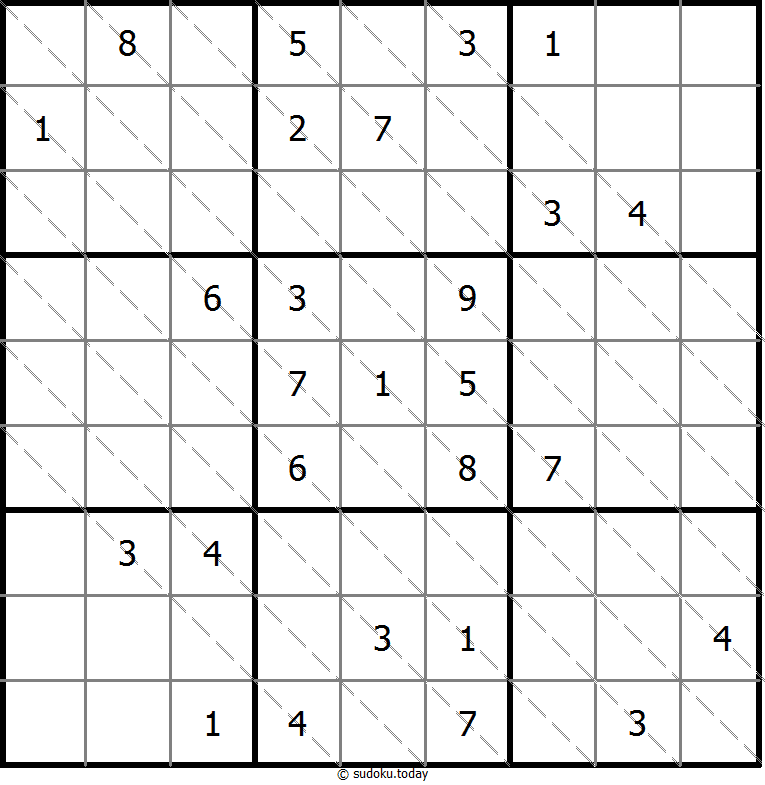
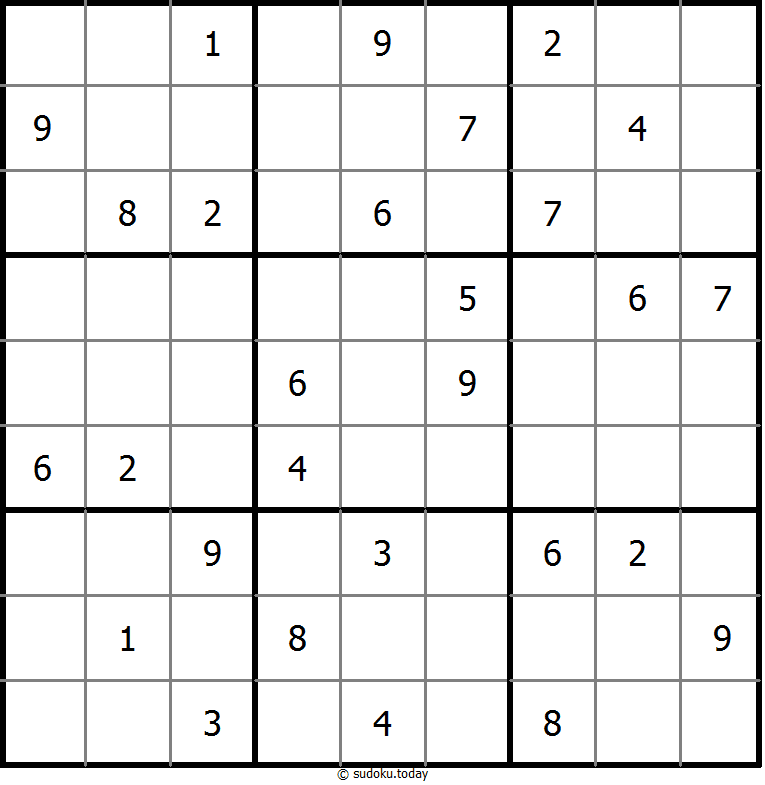
克隆数独
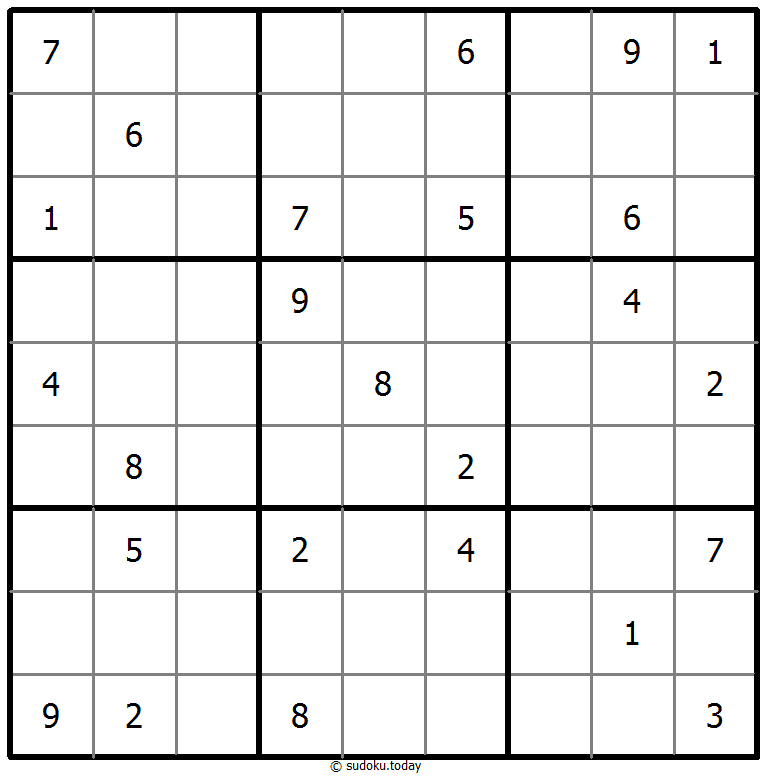
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
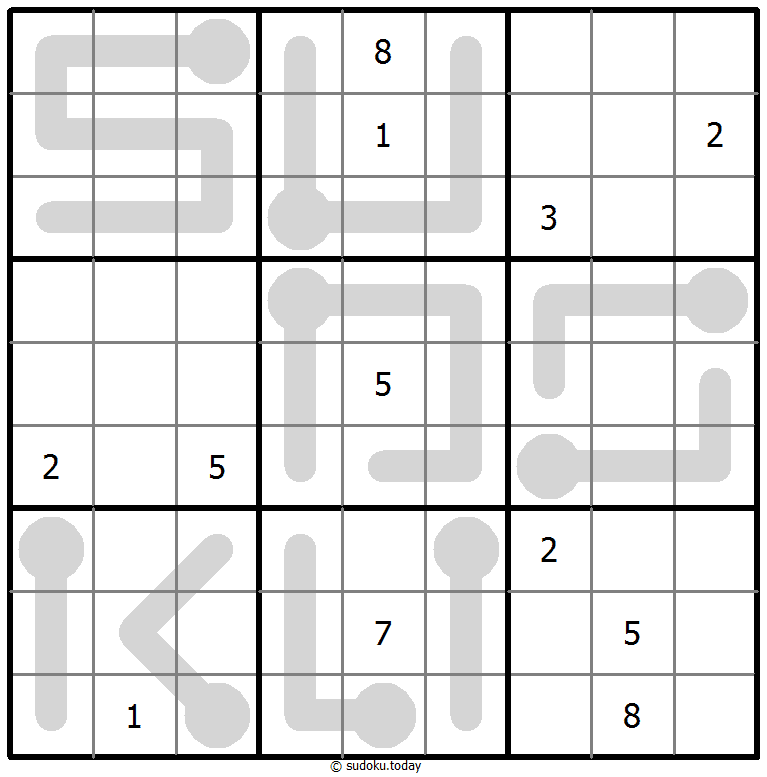
- 灰色标示出多块克隆(复制)区域。数字在这些克隆区域的相应位置上必须是相同的。这里说的克隆必须是平移的,不能是旋转或镜像的。
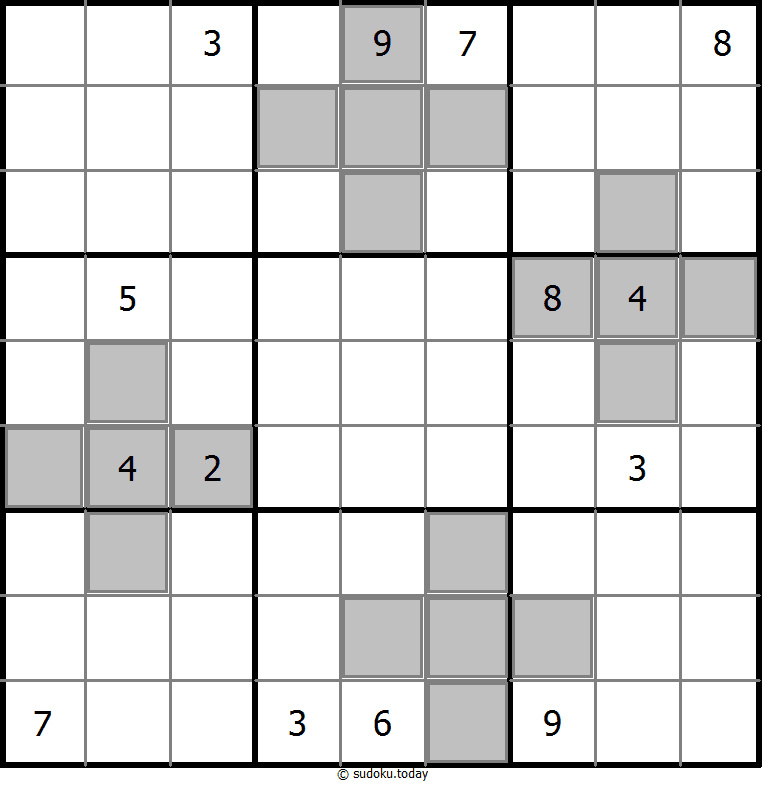
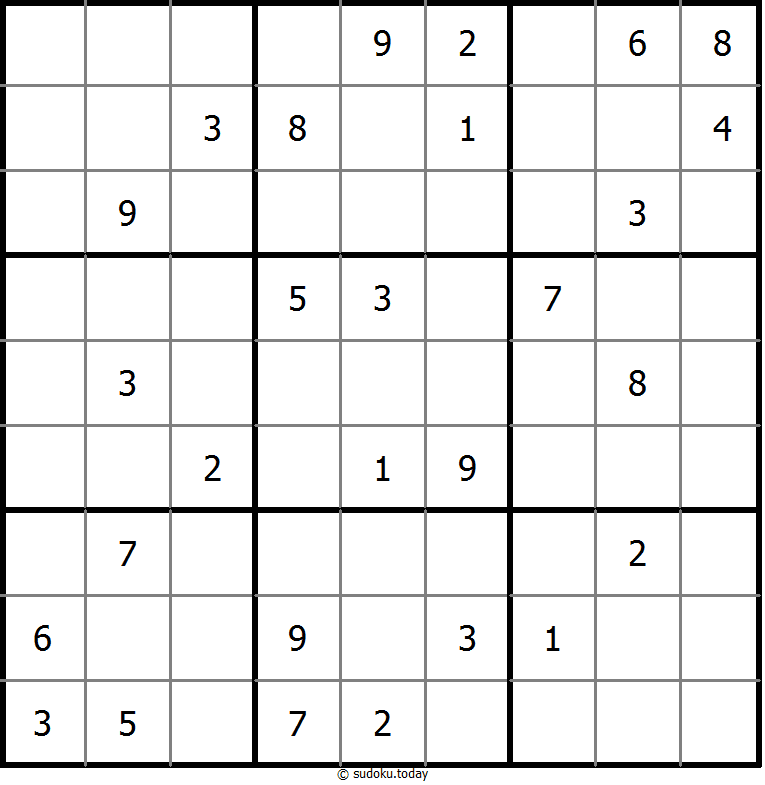
克隆数独
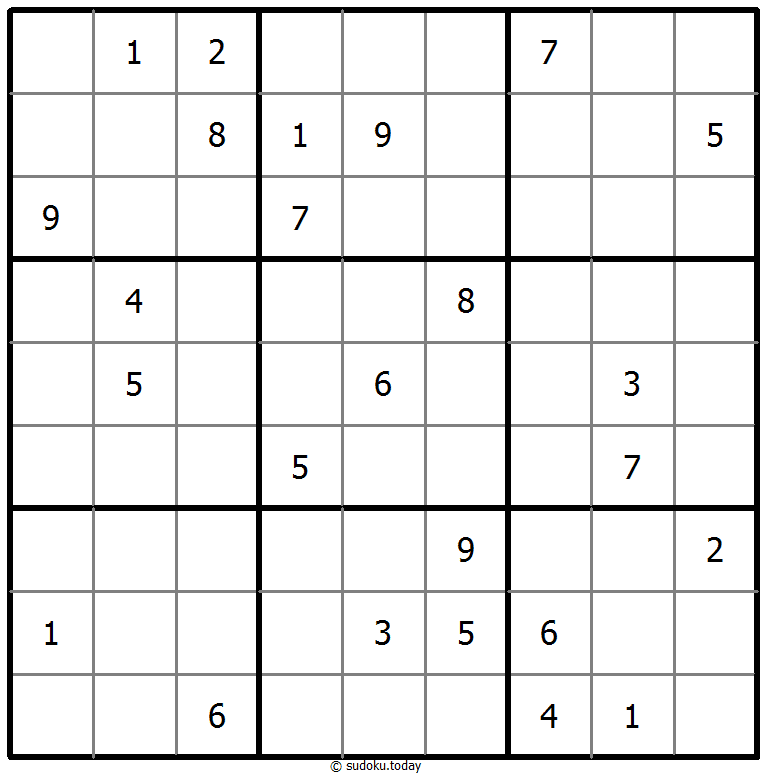
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 灰色标示出多块克隆(复制)区域。数字在这些克隆区域的相应位置上必须是相同的。这里说的克隆必须是平移的,不能是旋转或镜像的。
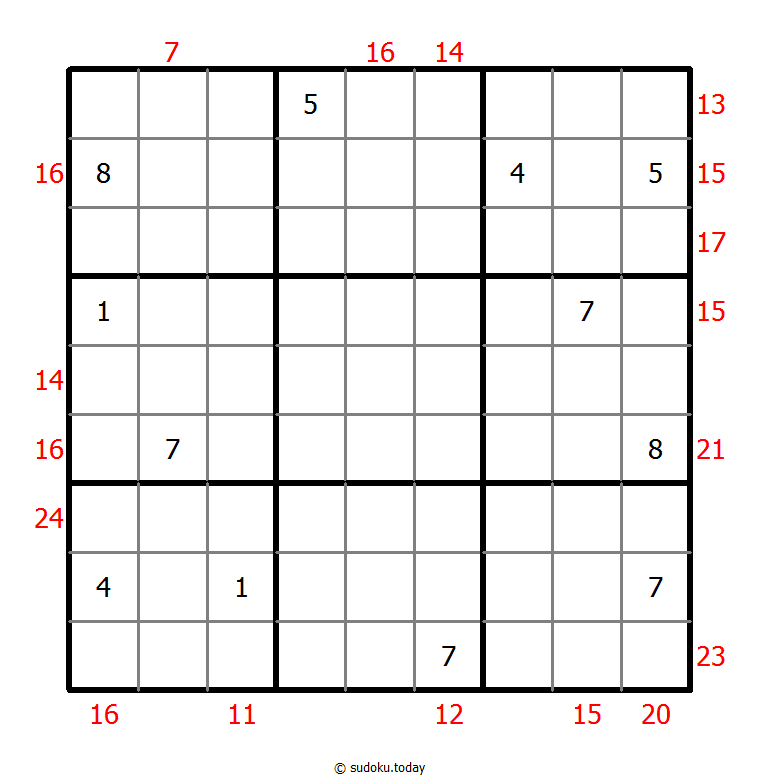
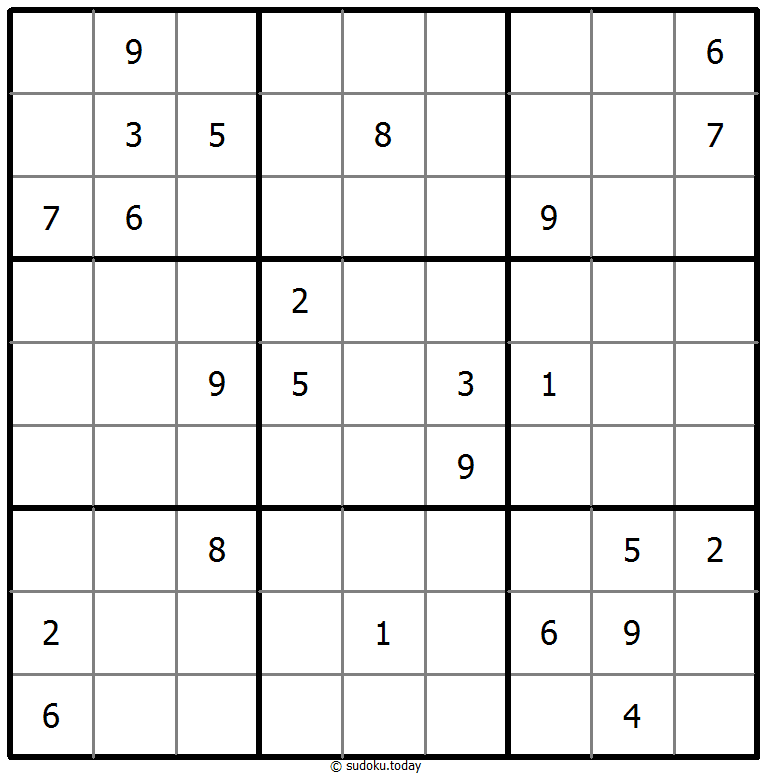
混合数独(XSum+连续)
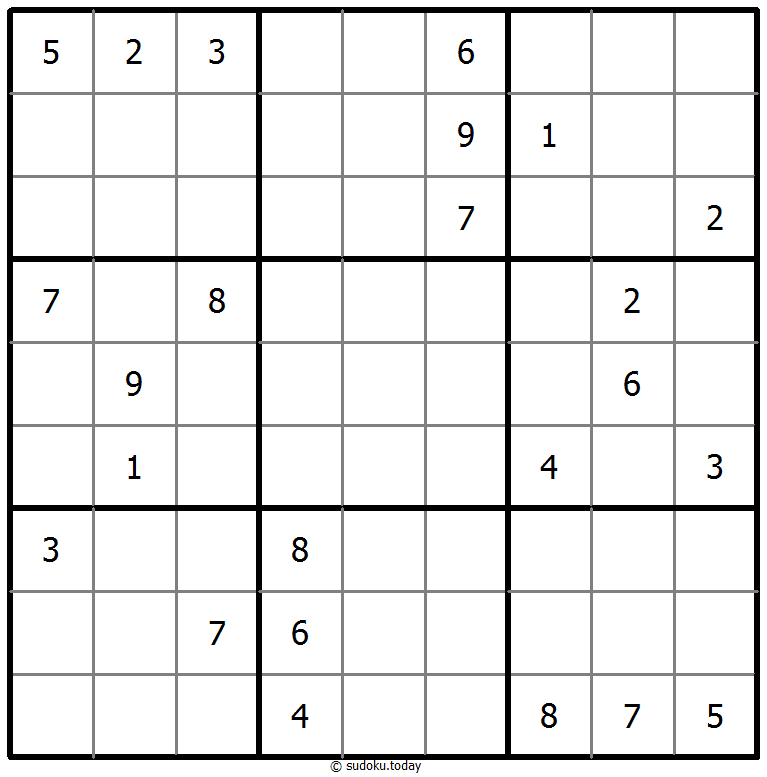
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 框格外的提示数代表其所在行(列)该方向上前X个数字之和,X等于该行(列)该位置方向上的第一个数字。
- 方框间有一些小点。点两边的数字必须是连续的。并非所有可能的点都有标记。
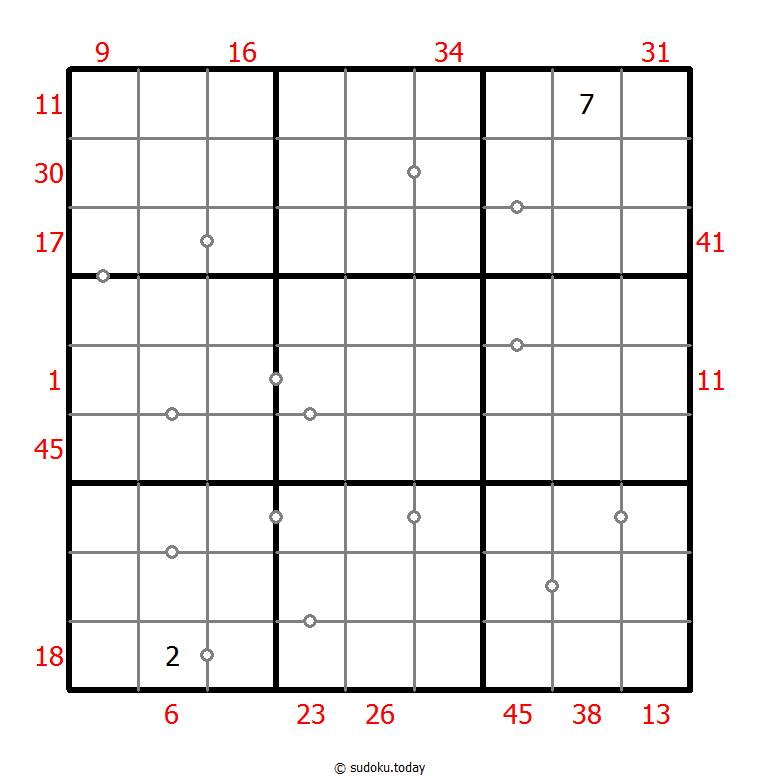
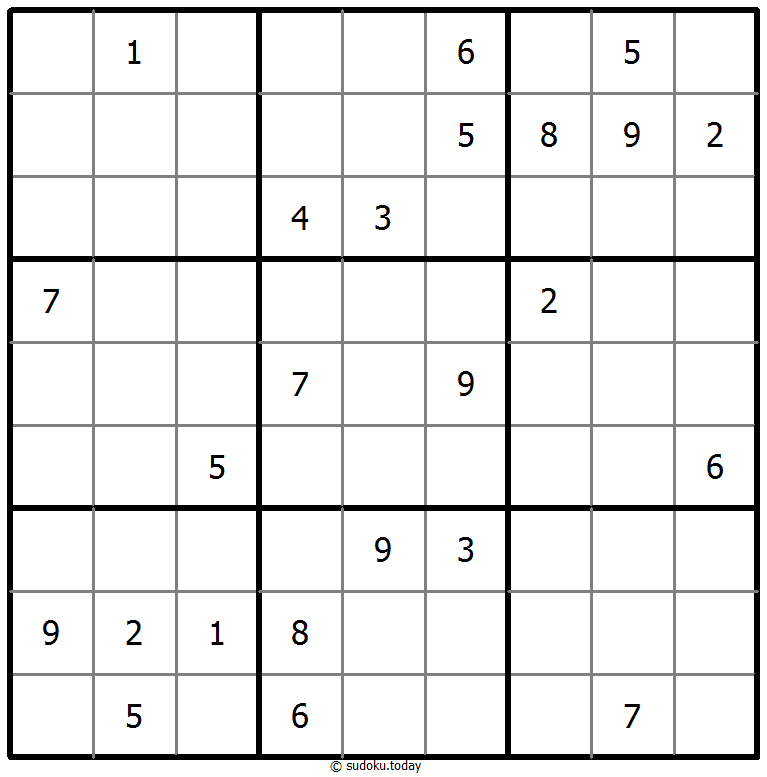
混合数独(XSum+连续)
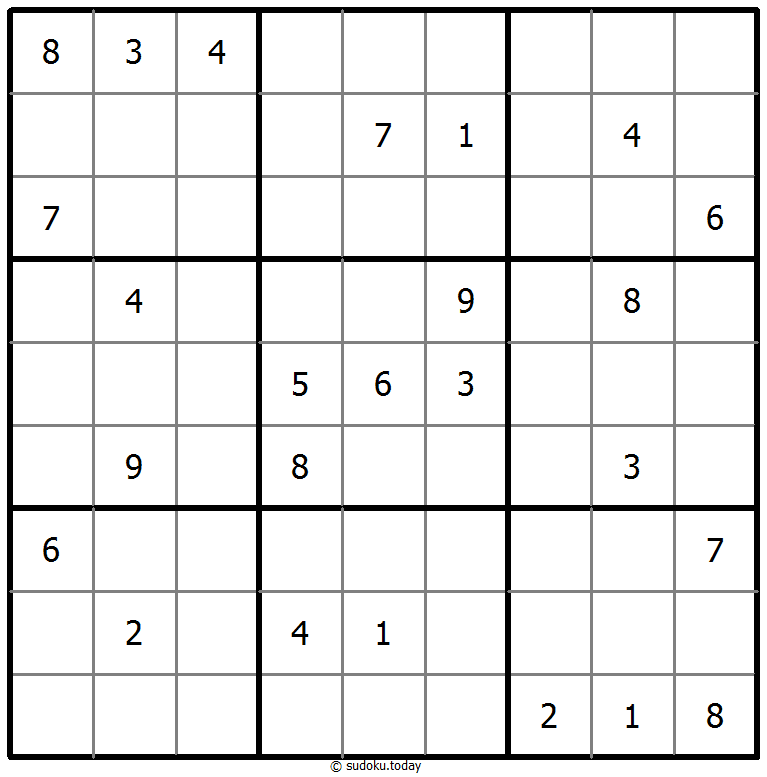
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 框格外的提示数代表其所在行(列)该方向上前X个数字之和,X等于该行(列)该位置方向上的第一个数字。
- 方框间有一些小点。点两边的数字必须是连续的。并非所有可能的点都有标记。
升序降序数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 网格外的箭头表示对应方向上最近的三位数字是升序还是降序(最高的数字总是在箭头的方向)。所有可能的箭头都给出了,因此如果没有箭头,则前三位数字在任何一个方向上都不会形成一个递增的序列。
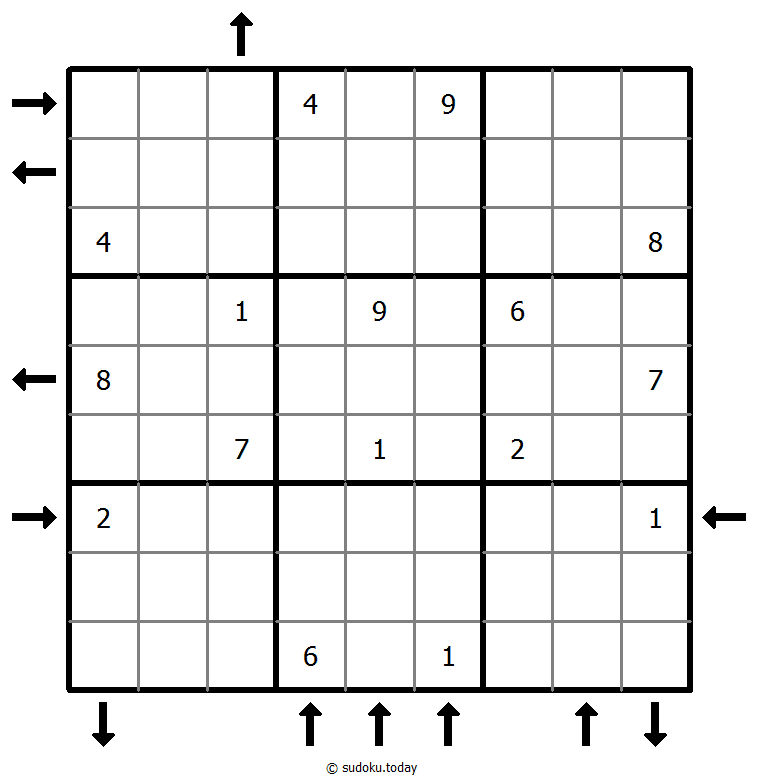
升序降序数独
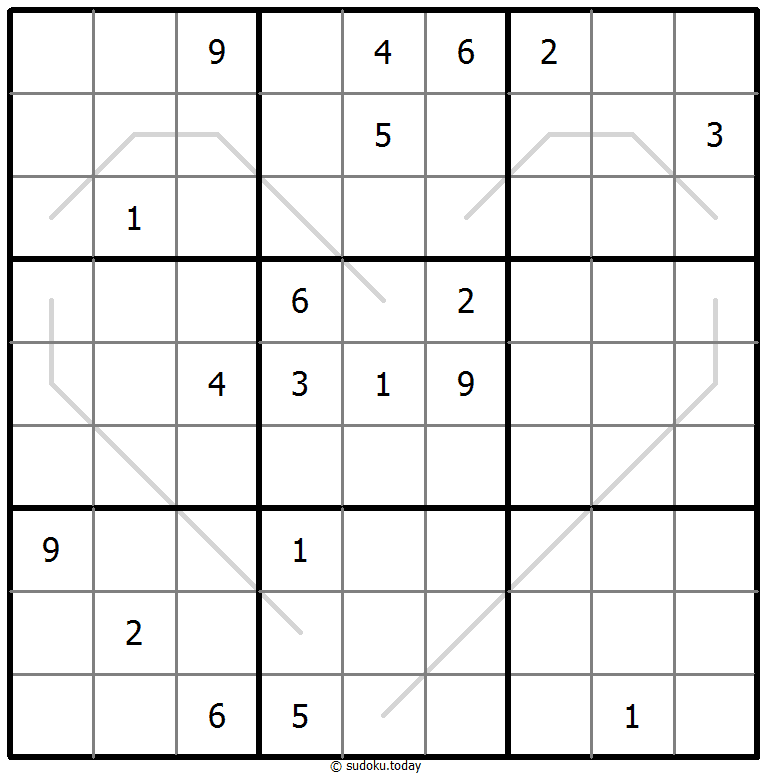
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 网格外的箭头表示对应方向上最近的三位数字是升序还是降序(最高的数字总是在箭头的方向)。所有可能的箭头都给出了,因此如果没有箭头,则前三位数字在任何一个方向上都不会形成一个递增的序列。
摩天大楼数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 把每一个数字看作是建筑物的高度。网格外的数字表示朝那个方向看时可以看到多少建筑物(较高的建筑物后面隐藏着较小的建筑物)。
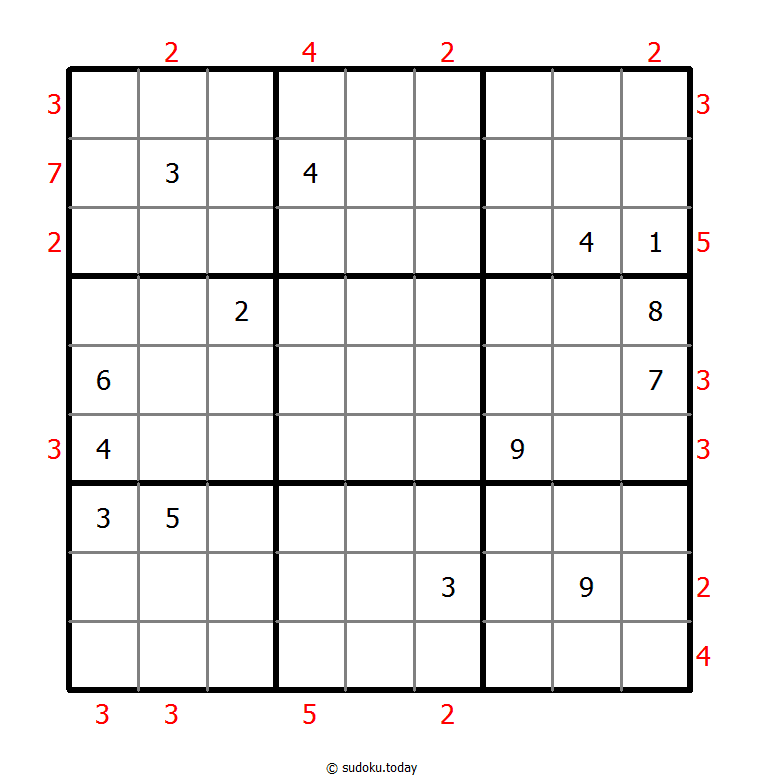
摩天大楼数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 把每一个数字看作是建筑物的高度。网格外的数字表示朝那个方向看时可以看到多少建筑物(较高的建筑物后面隐藏着较小的建筑物)。
Sujiken
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- Sujiken(来自日语sujikai,字面意思是“对角线”)是数独的变体。这个拼图由一个三角形网格组成,其中包含从1到9的数字。目标是用数字填充网格,这样每个单元格都包含一个数字,并且在任何列、行和任何方向的对角线中都不会重复数字。另外,三个较大的3×3正方形区域和由厚边界包围的三个较大三角形区域中的任何一个区域都不会出现两次数字。
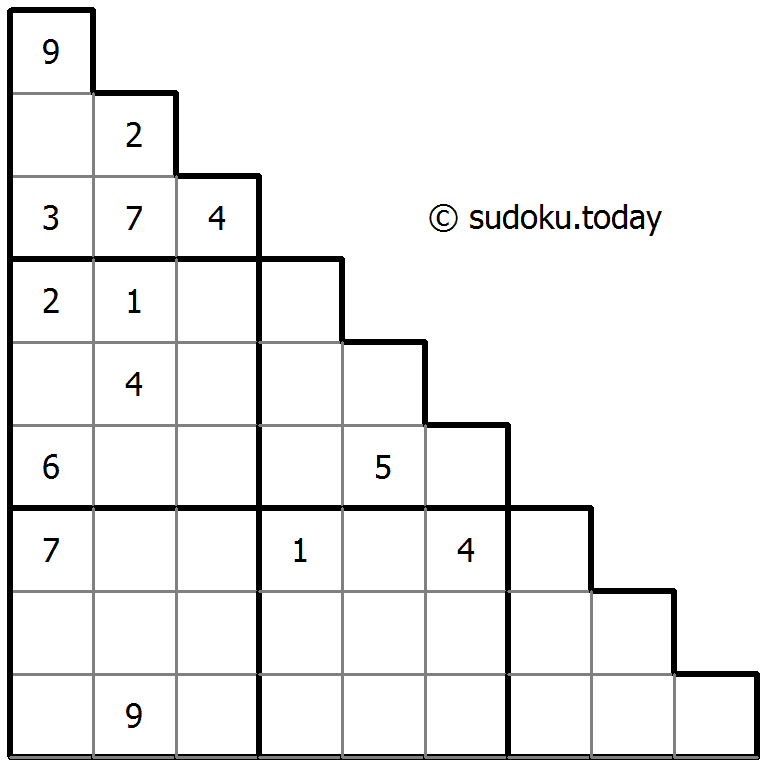
Sujiken
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- Sujiken(来自日语sujikai,字面意思是“对角线”)是数独的变体。这个拼图由一个三角形网格组成,其中包含从1到9的数字。目标是用数字填充网格,这样每个单元格都包含一个数字,并且在任何列、行和任何方向的对角线中都不会重复数字。另外,三个较大的3×3正方形区域和由厚边界包围的三个较大三角形区域中的任何一个区域都不会出现两次数字。
回答8数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
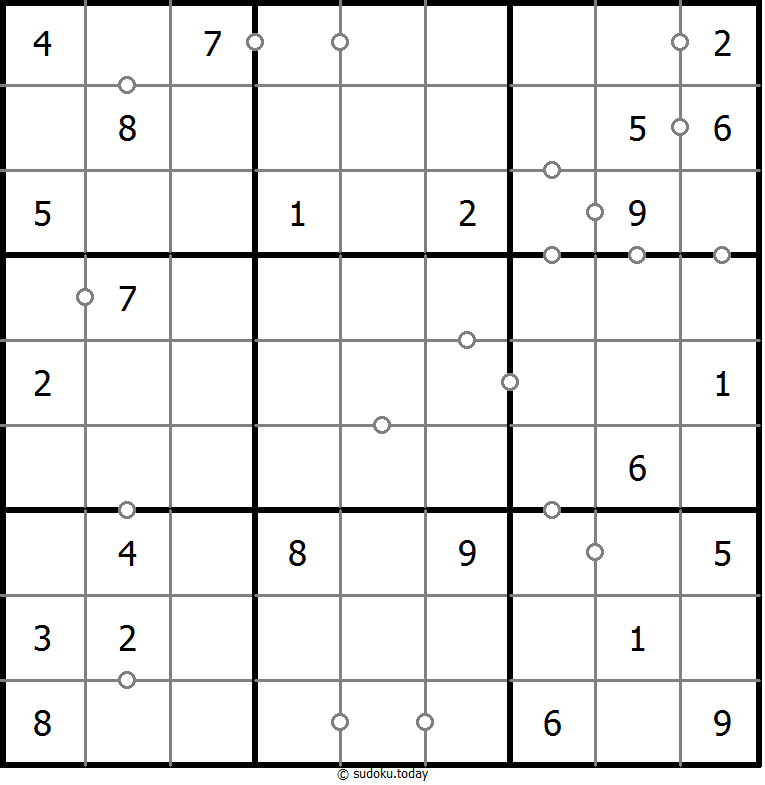
- 两个单元格之间的点表示这两个单元格中的数字的至少一个基本运算(加、减、乘、除)的结果是8。如果两个格子间没有点,则没有一个基本运算结果是8。
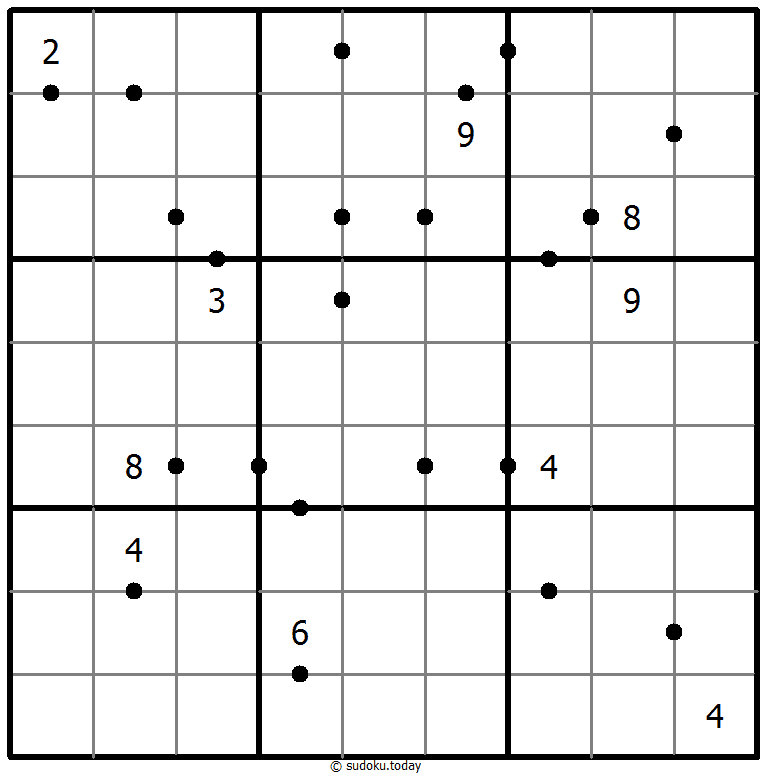
回答8数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 两个单元格之间的点表示这两个单元格中的数字的至少一个基本运算(加、减、乘、除)的结果是8。如果两个格子间没有点,则没有一个基本运算结果是8。
乘积数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 两个单元格之间的数字表示这些单元格中数字的乘积。四个单元格之间的数字表示两个对角相邻单元格(左上+右下(\)或右上+左下(/)之间的乘积。
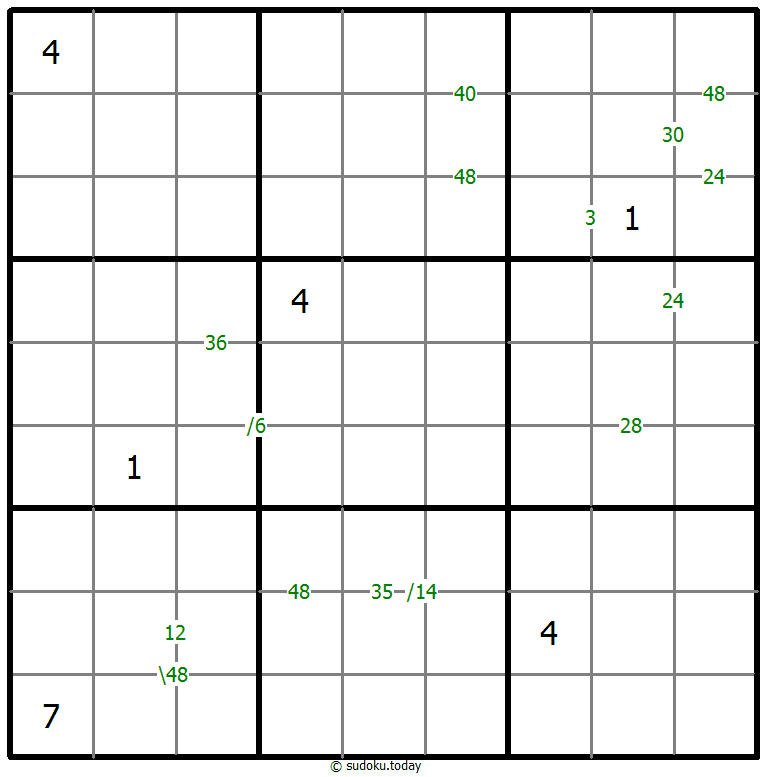
乘积数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 两个单元格之间的数字表示这些单元格中数字的乘积。四个单元格之间的数字表示两个对角相邻单元格(左上+右下(\)或右上+左下(/)之间的乘积。
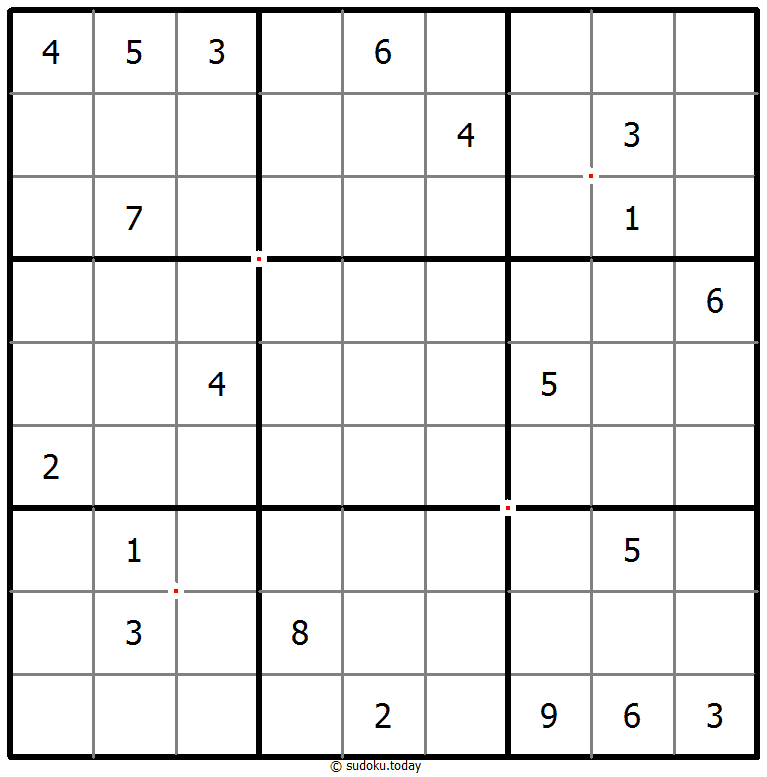
数学数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 网格线的某些交点用一个数字和一个运算符(+,-,x,/)标记在一个圆中。这个数字是运算的结果,适用于对角相对的两对单元格。圆圈中的“E”表示所有四个相邻数字均为偶数,而“O”表示所有四个相邻数字均为奇数。
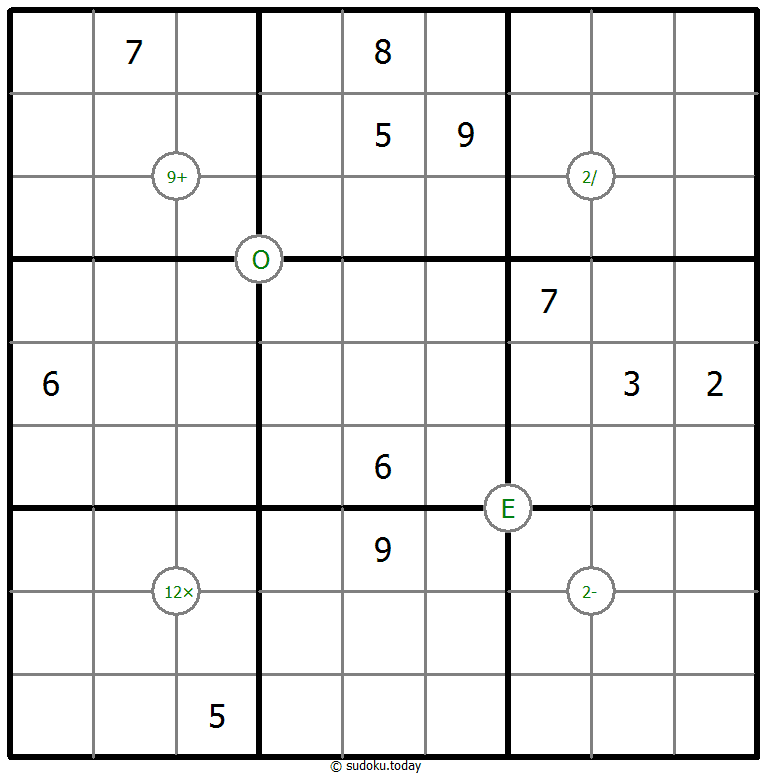
数学数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 网格线的某些交点用一个数字和一个运算符(+,-,x,/)标记在一个圆中。这个数字是运算的结果,适用于对角相对的两对单元格。圆圈中的“E”表示所有四个相邻数字均为偶数,而“O”表示所有四个相邻数字均为奇数。
双色蛋糕数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
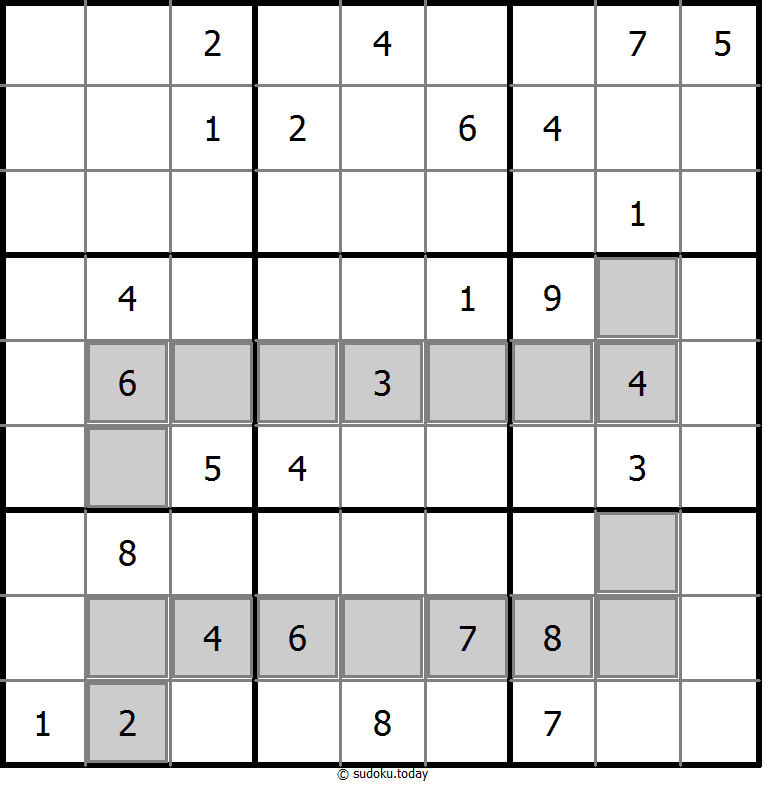
- 每2个奇数和2个偶数组成一个2x2棋盘图案,双色蛋糕标记已经给出。 双色蛋糕标记是2x2的单元格区域,其中左上角和右下角的单元格是一种类型,右上角和左下角的单元格是另一种类型。所有可能的点都有标记。
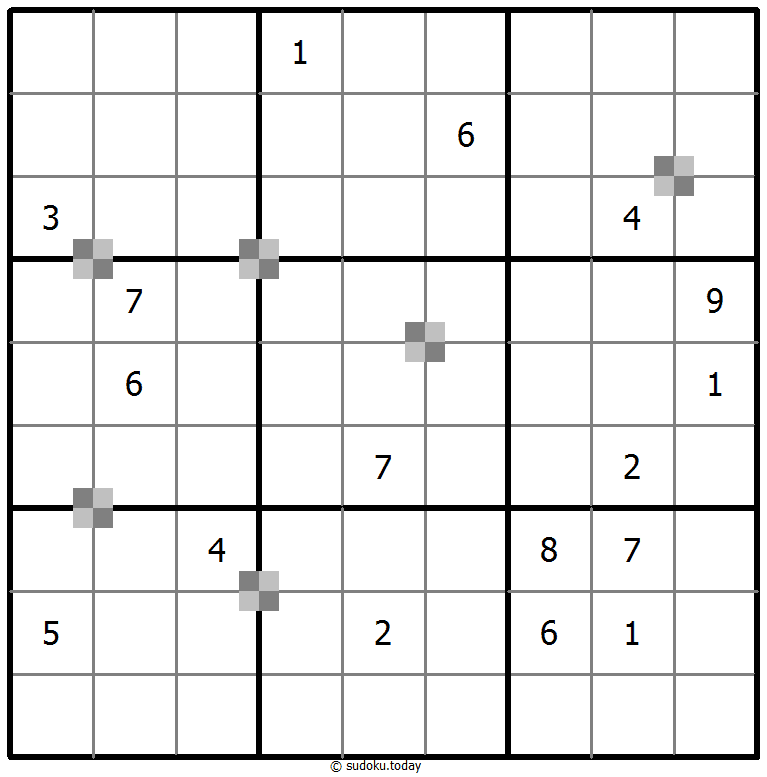
双色蛋糕数独
- 将1到9的数字放入每个空方块中,以便每个数字在每行、每列和9个3x3区域中恰好都出现一次。
- 每2个奇数和2个偶数组成一个2x2棋盘图案,双色蛋糕标记已经给出。 双色蛋糕标记是2x2的单元格区域,其中左上角和右下角的单元格是一种类型,右上角和左下角的单元格是另一种类型。所有可能的点都有标记。
English | 中文(简体) | 中文(繁體) | 日本語 | 한국어 | Français | Deutsch | Español | Português | Русский | Italiano | Nederlands | Türkçe | हिन्दी | ไทย | Tiếng Việt | Bahasa Indonesia | Polski | Українська |
数独 | Cool Sudoku | 数独 | Sudoku Puzzle | 賢くなるパズル
© sudoku.today All rights reserved 2019-2026